隨著科技走向,人們對于機械控制及航天工業的話題又逐漸火熱了起來,例如:臺灣福衛五號衛星的發射以及北朝鮮飛彈相關議題,也成為國際間討論的議題。然而,航天工業的進展,亦是一種國力的表現。而今天要大家討論的是一個在機械以及光電產業中較為冷僻但是卻在航天工業扮演相當重要角色的題目- 雷射光纖陀螺儀。
1817年,德國蒂賓根大學(University of Tübingen)的教授Johann Bohnenberger發表了史上第一個機械式陀螺儀,開啟了船舶導航的新紀元,,有別于過去的六分儀(利用星星以及太陽定位)以及指南針(利用地磁定位),人們對于船位以及航行方向可以有更精準的定位,大大增加了航行的可靠度以及安全性。圖一為建造于1914年,2010年以前號稱海上最大福音書城,當時被金氏世界紀錄認可為最老的運作中郵輪–忠仆號其導航之設備。

圖一、忠仆號其導航之設備。
經過人們對于光學以及物理學了解之后,1913年,法國物理學家Georges Sagnac提出了環形干涉儀的概念,利用左旋和右旋光線其光程差的不同,而得到位置的相關信息,相較于機械式陀螺儀,人們可以更精確的掌握船只自身的方位。然而,當時Sagnac的干涉儀體積過于龐大(圖二),對于實際應用而言,我們還需要將其積體化。
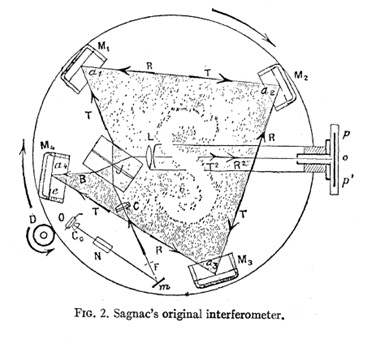
圖二、Sagnac實驗之架構圖[1]
一般而言,現代之光學陀螺儀可以分成環形雷射陀螺儀[2][3]、干涉式光纖陀螺儀 (I-FOGs)[4][5]、共振腔式光纖陀螺儀 (R-FOGs)[6][7],以及光子晶體陀螺儀[8][9]四部分。環形雷射陀螺儀系由一個在相同光程下具兩個相反傳播方向的環形雷射組成。雖然環形雷射陀螺儀在量測上具有高靈敏度,但卻因為體積太大,很難使用于實際應用上;此外,縮小環形雷射陀螺儀的體積也很困難[10][11]。而干涉式光纖陀螺儀(I-FOGs)是另一種使用光纖以增強Sagnac效應的環形干涉儀,被廣泛應用在導航上。當I-FOGs使用于導航時,需用到長度1-2公里的長程光纖,然而,長光纖會因溫度變化,而造成訊號飄移,這會降低光纖陀螺儀的性能表現 [6][12]。共振腔式陀螺儀(R-FOGs)是另一種利用被動式的環形共振腔用以取代主動式共振腔的陀螺儀。由于R-FOGs具有共振腔,所以其所需使用的光纖長度較I-FOGs短,R-FOGs的光纖長度通常只需要5-10公尺[7]。將R-FOGs與I-FOGs相比,可以發現前者所需使用的光纖數較少,且整體重量也較后者來得輕。隨著科技的逐年進步,光子晶體現已應用在陀螺儀上,B. Z. Steinberg以光子晶體為一可增強Sagnac相位的微小共振腔,光子晶體陀螺儀具有成為積體化組件的潛力[9]。然而,雖然R-FOGs與光子晶體陀螺儀具有縮小陀螺儀尺寸的潛力在,但它們的制程成本卻不低;另一方面,現代的光纖陀螺儀多采用可維持極化態的光纖(PMFs) ,使用這種光纖會使制造成本提高。
為此,結合光學外差干涉技術之雷射光纖陀螺儀即應運而生,我們研發了一外差振幅調制光纖陀螺儀,用以進行全動態偵測與利用較為便宜的單模光纖(SMFs)實現共光程架構。在此外差干涉陀螺儀的研究中,我們可以消除了SMFs造成的極化旋轉角,且使用SMFs可以節省成本;此外,由于這種光學設置具有使體積縮小的優點,所以可以應用在實際上。
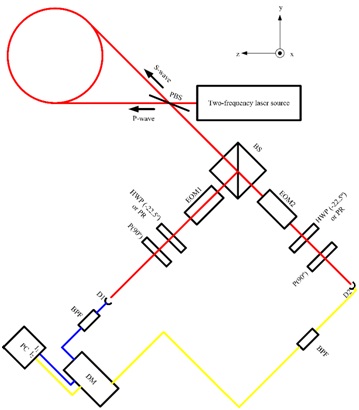
圖三、全動態范圍共光程外差平衡偵測式陀螺儀之光學架構
我們假設噪聲比為10-6,雷射波長為1550奈米,SMF長度為250公尺,而環形光纖的半徑是3.5公分。在此條件下,陀螺儀的零偏穩定度[注一]為0.872 deg/hr,我們可視具有此量級的陀螺儀為戰術級 (tactical grade)[注二][20]。和傳統型態的光纖陀螺儀相比,我們所需的光纖長度只需原來的1/4,相同的重量也會是傳統光纖陀螺儀的1/4,這意味著,利用此新型陀螺儀,我們可以有更多的空間酬載更多的設備在現今的航空器中。
此外差光纖陀螺儀可以提供全動態范圍的共光程架構和Sagnac相位量測,而和傳統的光纖陀螺儀相比,我們是第一個提出全動態范圍外差光纖陀螺儀的團隊。其中,共光程架構的特點可以改善傳統外差式I-FOGs的缺點[19],我們在計算中,SMFs造成的極化旋轉和共同噪聲可以被消除。然而,在SMF總光旋轉角為90?的情況下,通過SMF的雷射光會完全回到雷射源,這種情形會降低光學陀螺儀的信噪比,所以SMF的長度必須特別考慮;此外,為了校準相位,我們也必須量測得到入射偏振態的橢圓率;另外,SMFs的拍頻長度(beat length)也是重要的參數。一般而言,SMF的拍頻長度(beat length)的量級在公分等級,這表示光纖長度精準度的量級必須在公分以下。
在實際應用上,這個共光程外差平衡感測光纖陀螺儀可以被設計在芯片上;另一方面,使用SMFs也可以有效降低實驗成本。如圖二所示,我們將積體光學極化旋轉器[21]、偏振片[22]和偏振分光器[23]結合在沿Z傳播的Y切向鋰酸鈮晶體上,以建立一芯片式的雙頻外差光纖陀螺儀。由于SMFs具有短的拍頻長度(beat length),為了控制為一定值,所以必須特別注意SMFs的裝置過程與溫度控制。我們也可預期將我們的概念與高質量因子的共振腔兩者結合,可以制作出一外差式R-FOG[24],這類的外差式R-FOG具有重量輕、低成本,以及高性能導航工具的潛力。
展望未來,隨著人類對于太空探索以及國防產業的需求也越來越高,未來在航天議題的產業也隨之熱絡起來。希望在此波議題的帶領下,能有更多的廠商進入相關航天及國防產業的議題,提升技術能量。
參考數據
[1] 略
[2] S. Ezekiel and S. R. Balsamo, “Passive ring resonator laser gyroscope,” Appl. Phys. Lett. 30, pp. 478-480, 1977.
[3] W. W. Chow, J. Gea-Banacloche, and L. M. Pedrotti, V. E. Sanders, W. Schleich, and M. O. Scully, “The ring laser gyro,” Rev. Mod. Phys. 57, pp. 61-103, 1985.
[4] H. C. Lefèvre, “Fundamentals of the interferometric fiber-optic gyroscope,” Opt. Rev. 4, pp. 20-27, 1997.
[5] V. Vail and R. W. Shorthill, “Fiber ring interferometer,” Appl. Opt. 15, pp. 1099-1100, 1976.
[6] Z. H. Xie, Z.A. Jiang, S. S. Jian, and W. B. Tao, “Theoretical study on resonance characteristics of fiber optic ring resonator in fiber-optical ring resonator gyroscope,” Proc. SPIE 3552, pp. 267-271, 1998.
[7] X. L. Zhang, H. L. Ma, Z. H. Jin, and C. Ding, “Open-loop operation experiments in a resonator ?ber-optic gyro using the phase modulation spectroscopy technique,” Appl. Opt. 45, pp. 7961-7965, 2006.
[8] B. Z. Steinberg, “Rotating photonic crystals: A medium for compact optical gyroscopes,” Phys. Rev. E. 71, 056621, 2005.
[9] B. Z. Steinberg and A. Boag, “Aplitting of microcavity degenerate modes in rotating photonic crystals - the miniature optical gyroscopes,” J. Opt. Soc. Am. B. 24, pp. 142-151, 2007.
[10] F. Zarinetchi, S. P. Smith, and S. Ezekiel, “Simulated Brillouin fiber-optic laser gyroscope,” Opt. Lett. 15, pp. 229-231, 1991.
[11] J. Killpatrick, “The laser gyro,” IEEE Spectrum 4, pp. 44-54, 1967.
[12] K. Hotate, and M. Harumoto, “Resonator fiber optic gyro using digital serrodyne modulation,” J. Lightwave Technol. 15, pp. 466-473, 1997.
[13] S. M. F. Nee, C. J. Yu, J. S. Wu, and H. S. Huang, C. E. Lin, and C. Chou, “Heterodyne linear polarization modulation ellipsometer,” Opt. Express 16, pp. 4286-4295, 2008.
[14] C. Koch, “Measurement of ultrasonic pressure by heterodyne interferometry with a fiber-tip sensor,” Appl. Opt. 38, pp. 2812-2819, 1999.
[15] B. Sepulveda, A. Calle, L. M. Lechuga, and G. Armelles, “Highly sensitive detection of biomolecules with the magneto-optic surface-pasmon-resonance sensor,” Opt. Lett. 31, pp.1085-1087, 2006.
[16] K. Hotate, N. Okuma, M. Higashiguchi, and N. Niwa, “Rotation detection by optical heterodyne fiber gyro with frequency output,” Opt. Lett. 7, pp. 331-333, 1982.
[17] A. D. Kersey, A. C. Lewin, and D. A. Jackson, “Pseudo-heterodyne detection scheme for the fiber gyroscope,” Electron. Lett. 20, pp. 368-370, 1984.
[18] H. Koseki and Y. Ohtsuka, “Fiber-optic heterodyne gyroscope using two optical beams with orthogonally polarized components,” Opt. Lett. 13, pp. 785-787, 1988.
[19] H. Lefevre, The fiber-optic gyroscope, Artech House, Inc., Chap. 10, pp. 147-157, 1993.
[20] K. Kai, W. Zhang, W. Chen, K. Li, F. Dai, F. Cui, X. Wu, G. Ma and Q. Xiao, “The development of micro-gyroscope technology,” J. Micromech. Microeng. 19, 113001, 2009.
[21] A. V. Tsarev, “New compact polarization rotator in anisotropic LiNbO3 graded-index waveguide,” Opt. Exp. 16, pp. 1653-1658, 2008.
[22] T. Findakly, B. Chen, and D. Booher, “Single-mode integrated-optical polarizers in LiNbO3 and glass waveguide,” Opt. Lett. 8, pp. 641-643, 1983.
[23] K. G. Han, S. Kim, D. H. kim, J. C. Jo, and S. S. Choi, “Ti:LiNbO3 polarization splitters using an asymmetric branching waveguide,” Opt. Lett. 16, pp. 1086-1088, 1991.
[24] W. Y. Chiu, T. W. Huang, Y. H. Wu, Y. J. Chan, C. H. Hou, H. T. Chien, C. C. Chen, “A photonic crystal ring resonator formed by SOI nano-rods,” Opt. Exp. 15, pp. 15500-15506, 2007.
[注一]:零偏穩定度是當一個雷射光纖陀螺儀在靜止時量到的相位,理論上應該要為零,但實際上由于電子噪聲等因素,造成儀器會讀到相位值。所以我們在評估相關雷射光纖陀螺儀的性能時,零偏穩定度是一個相當重要的指針,其單位為deg/hr(簡而言之,就是一小時之內,相位漂移多少度)。
[注二]:根據零偏穩定度的大小,一般而言,我們可分為導航級、戰略級以及慣性級三種陀螺儀。
轉載請注明出處。








 相關文章
相關文章
 熱門資訊
熱門資訊
 精彩導讀
精彩導讀
























 關注我們
關注我們




