目前，大部分的衍射光柵產品均由母版復制而成，母版制備工藝主要有精密機械刻劃、可離子束增強的全息制版，另外也有一些諸如半導體光刻等新的科技手段。
延伸閱讀： 光柵基本原理【下】
光柵方程
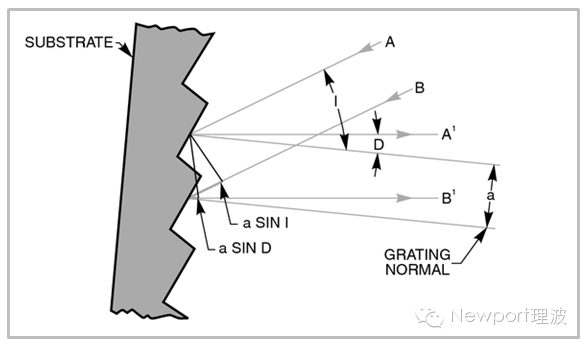
一個典型的衍射光柵包括基底（通常為光學材料），其表面通過加工形成的大量平行凹槽，以及表面鍍有的鋁膜等反射膜構成。凹槽的質量和間距是光柵參數的關鍵指標。若假定光柵表面與其刻劃方向正交的部分是鋸齒型，可以導出光柵基本方程。
波長為l的光束A和B，與光柵法線(Grating Normal)成角度I入射到相鄰凹槽。衍射光線A’和B’與光柵法線成角度D。二者光程差可表示為：
a sin I + a sin D
當光程差是波長l的任意整數倍時，光束A’和B’的疊加會產生相長干涉：
a(sin I + sin D) = mλ
其中m為整數，即衍射級數。
這是光柵基本方程。若D與I在光柵法線的兩邊，m取負值。
以上為假定只有兩凹槽的簡化情況，而綜合考慮其他所有凹槽，光柵衍射基本方程也不會改變，不過會增大衍射強度相對衍射角D的靈敏度。
圖1： 鋸齒型光柵
實際光柵方程
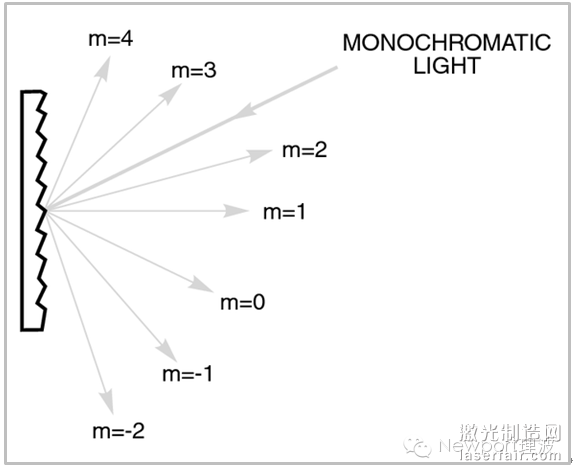
平行的單色光光束照射到光柵上，會產生不同級次的衍射，如圖2所示。在“光柵衍射級次”章節中將詳述。
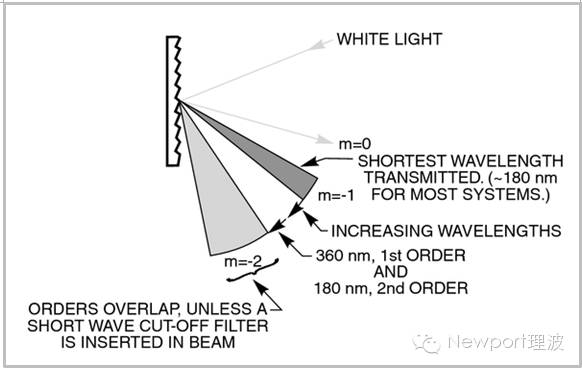
平行的多色光光束照射到光柵上，會產生色散，以使不同波長均滿足光柵方程，如圖3所示。
圖2.平行單色光滿足的光柵方程
圖3.經光柵衍射的多色光。圖中僅顯示負的衍射級次。
大部分單色儀中，入射狹縫和準直鏡確定了光柵入射光的方向，聚焦鏡和出射狹縫確定了出射光的方向。只有符合光柵方程的波長可以透過出射狹縫，其余的光在單色儀內被散射及吸收。雖然旋轉光柵會改變入射角I和衍射角D，但它們的差值始終保持恒定，這取決于單色儀的幾何構造。
單色儀更適用以下形式的光柵方程：
mλ = 2 x a x cos φ x sin θ
其中：φ =入射光衍射光夾角的一半
θ =光柵相對零級位置的角度
這些參數與入射角I和衍射角D的關系可表為
I = θ + φ，D = θ – φ
光柵衍射級次
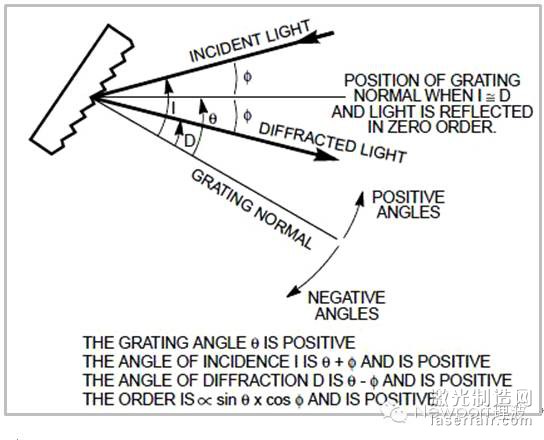
衍射級次“m”的正負可由任一形式的光柵方程決定。單色儀中，入射角I和衍射角D取決于光柵的旋轉。本文將所有在光柵法線逆時針方向的角度設定為正，順時針方向的設定為負，如圖4所示。半角φ始終為正。
如果D和I大小相同方向相反，光柵角度和級次均為0，光束全部被反射。當光柵角度為正時級次為正（m=1），反之級次為負（m=-1）。
當|m|>1時，光柵方程在高級次下亦成立，如m = ±2時λ2=λ1/2，m = ±3時λ3 = λ1/3等。λ2 和λ3即屬于二級和三級對應的波長，定義由圖3給出。
實際應用通常只需要一級衍射，其他高級次下的波長需要被濾除。入射光譜范圍和探測器的靈敏度決定了是否需要使用選通或截止濾光片。
圖4.對入射角I、衍射角D和光柵角q的正負的定義。
延伸閱讀： 光柵基本原理【下】
轉載請注明出處。
相關文章
熱門資訊
精彩導讀
關注我們
