激光束腰和分布
       為了獲得高斯光束光學的精確原理和限制，有必要理解激光束輸出的特性。在TEM（橫模和縱模為0）模式下，光是從激光開始輻射，就像一個含有高斯橫截發光剖面的完美平面波，如下圖顯示。高斯形狀被激光內部的尺寸或者某種光學序列的限制光圈在某個直徑處被截斷。為了指定和論述激光光束的傳播特性，我們必須給它的直徑下一些定義。普遍被采用的定義是光束發光（最強烈）峰值，軸向或者數值的地方的直徑衰減1/e2（13.5%）。

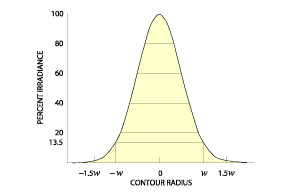
       衍射效應使光在傳播過程中向橫向傳播。因此它不可能有一個被精確校準的光束。激光光束的傳播可以被純衍射理論精確地預測。異常現象小到在這里可以統統不用去考慮。在非常平常的情況下，光束傳播可以小到被忽略。下面的方程精確地描述了光束的傳播，由此可以很容易地看出激光光束的能力和限制。

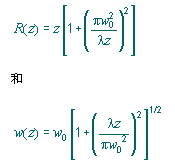
        即使一個高斯TEM（橫模和縱模為0）激光光束波陣面在某個平面可以保持非常的平坦，它也需要彎曲并且通過如下的公式傳播
       這里的z是當波陣面平坦時從平面上的傳播路徑，l是光的波長，w是當波陣面平坦時，在平面上1/e2發光輪廓的半徑，w(z)是在波傳播了距離z以后，1/e2輪廓的半徑，R(z)是在波傳播了距離z以后，波陣面的曲率半徑。在z=0的條件下，R(z)是無窮大的，在某種有限的z的最小值內傳播，并且當z進一步增大的時候，趨近于無窮大。Z=0平面標記了高斯腰的位置，或者表示波陣面是平坦的地方，這里w0叫做光束腰半徑。

高斯TEM光束的發光分布按如下方式定義 

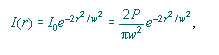
       這里的w=w(z)和P是光束的總功率，在所有的相交的部分是等值的。分布形式的恒定性是對在z=0的時候高斯分布預測的特殊結果。如果統一的發光分布在z=0時刻被預測，z=∞時刻的形式將與貝塞爾公式給出的艾利斑（Airy disc）形式相似，這里z值中間的形式將變得非常復雜。
       這里假定z遠大于pw0 /l，因此1/e2發光輪廓漸漸逼近一個圓錐形的角半徑

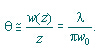
       這個值是一個高斯TEM光束的遠場角半徑。圓錐的頂點在腰的中心位置，如下圖所示。

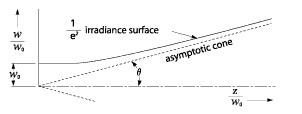
       需要注意的是，在給定l值得條件下，不大可能表示出光束直徑的變化和分布，在距離z作為一個獨立參數運行時，W0，光束腰半徑。

近場和遠場的分別
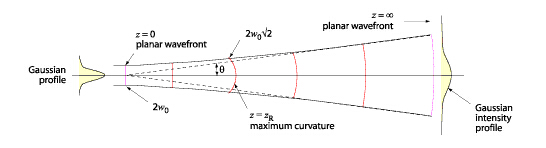
       不像常規的光束一樣，高斯光束不是線性的分布。靠近激光的時候，分布角度是非常的小的。遠離激光的時候，分布角如上描述接近漸進的限制。在瑞利判據范圍，定義為光束半徑通過2的平方根因素傳播的距離，在下面式中給出

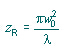
       在光束腰(z = 0)的地方，波陣面更加平坦。同樣地，在z = ∞處，波陣面也更加平坦(R(∞) = ∞).。隨著光束從腰部傳播，波陣面的曲率因此必須增加到最大值并且緊接著開始下降，如下圖所示。Raleigh范圍，考慮到在近場分布和中波段分布之間的區分線，是從波陣面曲率最大值腰部的距離。遠場分布（數值查詢激光器說明）必須在遠大于ZR（通常大于10nbsp即足夠）的時刻才能別測量。這是非常重要的區別，因為在一個光學序列中對點大小和其它參數的計算會在近場或者中場分布被使用時變得不準確。對于一個緊緊被聚焦的光束，從腰部（聚焦點）到遠場的距離僅僅是幾毫米或者更小。對于從激光直射光束，遠場距離可以按米的數量級來測量。